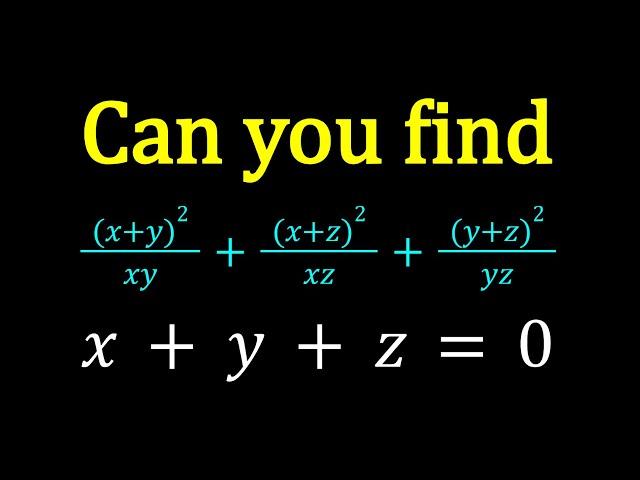
Let's Simplify A Rational Expression

Let's Simplify A Rational Expression

SyberMath Shorts

1 месяц назад

1,073 Просмотров
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
https://www.youtube.com/@SyberMath
https://www.youtube.com/@aplusbi

⭐ Join this channel to get access to perks:→ https://bit.ly/3cBgfR1
My merch → https://teespring.com/stores/sybermath?page=1
Follow me → https://twitter.com/SyberMath
Subscribe → https://www.youtube.com/SyberMath?sub_confirmation=1
⭐ Suggest → https://forms.gle/A5bGhTyZqYw937W58
If you need to post a picture of your solution or idea:
https://twitter.com/intent/tweet?text=@SyberMath
#algebra #polynomials #rational
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva

PLAYLISTS 🎵 :
▶ Trigonometry: https://www.youtube.com/playlist?list=PLU0ULtGEndnxL0r6NaxQKILn3OSqOzbiN
▶ Algebra: https://www.youtube.com/playlist?list=PLU0ULtGEndnxX7K9TRSmMssUv_3_31jIl
▶ Complex Numbers: https://www.youtube.com/playlist?list=PLU0ULtGEndnwpHFjKPFj-8J8GOtOP8EV4
▶ Calculus: https://www.youtube.com/playlist?list=PLU0ULtGEndnyXE1Ta-sVT3upREagueUQH
▶ Geometry: https://www.youtube.com/playlist?list=PLU0ULtGEndnxWWVtx7PZHUQv1wrW9rGy2
▶ Sequences And Series: https://www.youtube.com/playlist?list=PLU0ULtGEndnzL0sDmaBL1Kjm_2uC3HcD7
Ссылки и html тэги не поддерживаются

Комментарии:

@phill3986
@phill3986 - 14.09.2024 17:57

👍☮️✌️😃😎😃✌️☮️👍

Ответить
@MrGeorge1896
@MrGeorge1896 - 14.09.2024 18:42

Method 3:
Expand the squares and divide by the denominators gives
x/y + 2 + y/x +x/z + 2 + z/x + y/z + 2 + z/y
= 6 + (y + z) / x + (x + z) / y + (x + y) / z
= 6 + (-x) / x + (-y) / y + (-z) / z
= 6 - 3
= 3

Ответить
@nasrullahhusnan2289
@nasrullahhusnan2289 - 15.09.2024 16:48

x+y+z=0
Let a=[(x+y)²/xy]+[(x+z)²/xz]
+[(y+z)²/yz]
=(z²/xy)+(y²/xz)+(x²/yz)
=(x³+y³+z³)/xyz
0=(x+y+z)³ as x+y+z=0
=x³+y³+z³+3(x+y+z)(xy+yz+zx)
-3xyz
=x³+y³+z³-3xyz
(x³+y³+z³)/xyz=3 --> a=3

Ответить
Сейчас смотрят
Let's Simplify A Rational Expression 08:23
Let's Simplify A Rational Expression SyberMath Shorts
NVDA多头开始恐慌了？ #nvda #美股 0:18
NVDA多头开始恐慌了？ #nvda #美股 小左美股第一视角
Japanese technique - How to fillet a whole salmon - 鮭のさばき方 5:49
Japanese technique - How to fillet a whole salmon - 鮭のさばき方 Cooking with Chef Dai
Save Some Money, Hardkorr 3000W Inverter - IS THERE ANY BETTER?? 12:57
Save Some Money, Hardkorr 3000W Inverter - IS THERE ANY BETTER?? Off Track
Amyra Dastur Snapped At Dance Class In Bandra | 10 TV Live 0:49
Amyra Dastur Snapped At Dance Class In Bandra | 10 TV Live 10TV LIFE
Aparat pentru vata de zahar, vintage 0:23
Aparat pentru vata de zahar, vintage RomaniaMag
ᱚᱞ ᱪᱤᱠᱤ ᱨᱮᱭᱟᱜ ᱜᱚᱲᱦᱚᱱ // ᱥᱟᱹᱜᱟᱹᱭ ᱯᱮᱲᱟ 5:14
ᱚᱞ ᱪᱤᱠᱤ ᱨᱮᱭᱟᱜ ᱜᱚᱲᱦᱚᱱ // ᱥᱟᱹᱜᱟᱹᱭ ᱯᱮᱲᱟ ᱥᱟ.ᱜᱟ.ᱭ ᱯᱮᱲᱟ
BZR-X Driving Lights | The Best Driving Light Ever Created? Probably. 1:37
BZR-X Driving Lights | The Best Driving Light Ever Created? Probably. Hardkorr
DÜNYANIN EN BÜYÜK LUNAPARKI! 14:26
DÜNYANIN EN BÜYÜK LUNAPARKI! Orkun Işıtmak
KITA MEMBUAT RUANGAN RAHASIA YANG TERSEBUNYI!! 11:51
KITA MEMBUAT RUANGAN RAHASIA YANG TERSEBUNYI!! Alviand Miracle
MANCING IKAN BUAT PESTA MAKAN BARENG KELUARGA!! DAPAT BNYAK GUYS!! 12:02
MANCING IKAN BUAT PESTA MAKAN BARENG KELUARGA!! DAPAT BNYAK GUYS!! Alviand Miracle
Which is Best? Enerdrive 40Amp+ or Hardkorr 40Amp DCDC Charger 5:12
Which is Best? Enerdrive 40Amp+ or Hardkorr 40Amp DCDC Charger Off Track