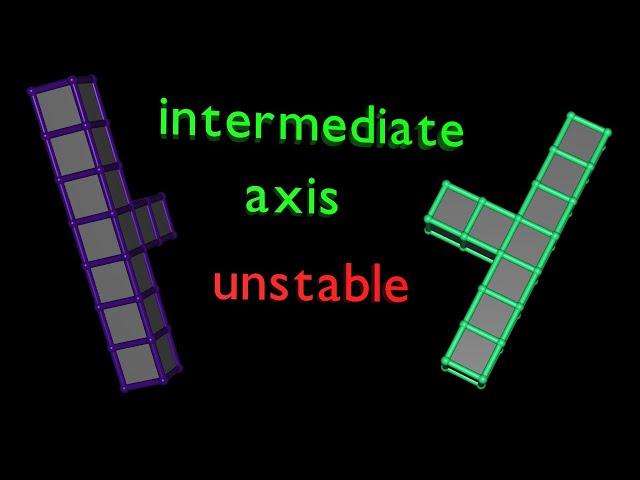
Tennis racquet flip

The tennis racket theorem (intermediate axis theorem or Dzhanibekov effect) visualized for various initial conditions and moment of inertia. The effect is described by the unstable rotation around the second principal axis associated with the apparent and rapid flip of freely rotating rigid bodies.

The effect is visualized by the Poinsot's ellipsoid, which is here normalized to a sphere and projected onto a plane. Rigid body dynamics are visually presented on both the sphere and the plane for both vastly different initial conditions as well as small perturbations. All shown rigid bodies have the same energy.

The rigid bodies are constructed from solid unit cubes. They are simulated using Hamilton's equations of the Hamiltonian system expressed in four quaternion coordinates and conjugate momenta allowing fast and accurate simulations regardless of initial conditions.

The simulations were performed using high order explicit symplectic integrators and were rendered in real time.

🎵 "3D Galax" (amiga version) by "Ben Daglish" aka "Benn" | not affiliated with/endorsed by.

Тэги:

#tennis_racket #tennis_racket_theorem #intermediate_axis #intermediate_axis_theorem #rigid_body #rigid_body_dynamics #dynamical_system #Dzhanibekov_effect #Poinsot #Dzhanibekov #dynamics #rigid #hamiltonian #lagrangian #classical_mechanics #Louis_Poinsot #stereographic #quaternion #rotation

Скачать видео