El Mayor Problema de la Computación SIN RESOLVER

Excelente, me encanto la forma y toda la informacion, increible, muy bueno 🔥🔥🔥🔥🔥🔥
Excelente, me encanto la forma y toda la informacion, increible, muy bueno 🔥🔥🔥🔥🔥🔥
Excelente, me encanto la forma y toda la informacion, increible, muy bueno 🔥🔥🔥🔥🔥🔥

Yo tengo la solución y demostración 1k likes y lo demuestro en un vídeo

En realidad ya he resuelto el problema P vs. NP:
P=NP
P-NP=0
(1-N)P=0
O sea que NP=P si y solo si P=0 o N=1.
¿Dónde está mi millón de dólares?

Esta afirmación de Mike es correcta?, es decir, entiendo que hizo el despeje de la variable N y P y aquello le dio un resultado, pero mi pregunta es ¿saber esto sirve de algo o a partir de aquí que es lo que seguiría?... no es broma jsjs, tengo esa duda

Aqui sois todos muy inteligentes pero más de uno esta inyectado con nanotecnología y ni lo sabe aún...

Como estudiante de 2° Bachillerato puede que esté diciendo alguna barbaridad por falta de conocimientos, pero... ¿no se podría averiguar si se cumple o no la igualdad partiendo de ambas premisas? 👀

En todo caso, sería ver qué "cambia" el hecho de que lo sea o no (ligeras variaciones).

Por ejemplo, yo cuando quiero saber si un problema es "A" o "B" dirijo la atención al resultado que me darían ambas premisas (algo así como cuando en el laberinto que dan en los manteles de restaurantes encuentras el camino correcto partiendo del final).

Tal vez sea algo estúpido y ya alguien lo haya refutado, pero bueno... 🤷

Viendo esto cuando yo me confundo con las fracciones....

El arco de los tatakai del milenio :v

A ver si lo he entendido, en resumen: lo que quieren es hacer un algoritmo que de directamente la comprobación de algo np sin tener que ir comprobando uno por uno. Es eso?, Y si no lo es no me funen, fue lo que entendí, sorry.

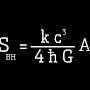
excelente video

a ver si entendi, si hallo el algoritmo para hacer el problema de las damas para cualquier posicion, me voy a llevar 1m de dolares?

Después de saber programar en varios lenguajes de programacion de distintos paradigmas aún no entiendo el problema en su totalidad. Pero lo explicaste genial. Es el mejor video explicativo del problema

O sea, para que P≠NP el algoritmo NP no debe tener ni una solución P y ni se pueda reducir de forma polinómica a un NP-Completo. Verdad???

para el ajedrez, las reinas se disponen en L, por tanto el algoritmo de verificacion debe seguir el mismo camino de colocacion de fichas original. Similar al tema de compresion de archivos, con un diccionario igual al archivo input, el archivo input no usa mas espacio q una referencia.

Mike que libro recomiendas para estudiar este tema en particular, un poco mas en profundidad, desde ya muchas gracias, soy estudiante de Ciencias Computacionales en la UBA(Universidad de Buenos Aires), y me apasiono bastante este tema, y también el millón de dólares ...

No existe demostración de P vs NP por un error del álgebra: El álgebra no es un algoritmo sino un pseudo -algoritmo. Considera un subconjunto de las leyes de la lógica, pero no todas. Y para resolver P vs NP se requiere lógica completa.
La ley que no respetan el álgebra ni la aritmética es que, sí algo es lógico, se puede construir un mecanismo que lo haga y viceversa: si un mecanismo consigue algo, es porque ese algo es válido. Por el contrario si algo no posee lógica no se puede construir o diseñar un mecanismo para ello y viceversa: si no se puede diseñar el mecanismo que logre algo, ese algo no posee lógica. Y es importante porque es imposible diseñar un mecanismo que cuente hasta infinito, lo que implica que incluso la ley de gravedad está planteada de forma errónea, ya que tiende a infinito en un agujero negro. Pero se lo soluciona fácilmente agregando una variable, conocida según el tipo de mecanismo, como voltaje, presión, torque, etc.
Volviendo a P vs NP, la eficiencia de un algoritmo está sujeta primero al diseño de la máquina que lo ejecutará. Un procesador de 32 bits resuelve una suma de 32 bits en un único ciclo de reloj, pero requiere más ciclos para sumas más grandes, lo que vuelve a P algo relativo con tendencia a NP.
Pero, más allá de éso, es imposible diseñar una máquina que resuelva en un único ciclo problemas que:
A- se desconozca desde un inicio la cantidad de elementos involucrados o Dada una máquina de cierta capacidad, no se puedan completar los sobrantes con elementos nulos. Por ejemplo es imposible resolver una división de forma directa porque no se sabe con anticipación cuántos decimales arrojará. Excepto que se límite la precisión arbitrariamente.
B- Algún elemento del problema afecte el resultado de uno que ya fue procesado. Ésto implica que el problema solo se puede resolver mediante una máquina de cambios de estado, es decir un ciclo en el cual cada ciclo provee información al ciclo siguiente, hasta llegar a un resultado final.
Y ese es todo el misterio de P vs NP, pero no puede haber una demostración, porque el álgebra considera posible una máquina que haga lo imposible.

¿Sabe qué?... Voy a cambiar el enfoque, porque decir "es un error del álgebra" puede ofender a alguno por ahí. Lo explicaré de otra forma: No se puede demostrar P vs NP porque la solución cambia según las reglas que especifiques para el problema. Me explico:
Imaginemos por un momento que es posible construir una máquina cuya capacidad de procesamiento fuese inferior a un bit. A medida que reducimos la capacidad hacia el infinitesimal de bit, todos los problemas para ésa máquina en particular tienden a ser NP, hasta llegar al punto teórico en que cualquier problema le lleva infinidad de tiempo el resolverlo. Si bien es sencillo comprender que éso no es posible, porque la menor unidad de procesamiento posible es el bit, no hay cómo explicarle éso al álgebra. Es una regla de validez que se debe establecer por encima de cualquier resultado que el álgebra nos pueda dar.
¿Qué hay por el otro lado? Para una máquina con capacidad de procesamiento infinita, cualquier problema es P. De hecho, ésa máquina no necesitaría calcular nada, porque para cualquier problema que le pudiésemos plantear ya tendría la solución alojada en algún lugar de su memoria. Así que obtener cualquier respuesta solo sería buscar y dar.
Pero éste extremo es imposible y, de nuevo, no es factible decírselo al álgebra. De hecho ¿En qué punto la complejidad de una máquina se vuelve siquiera irrazonable? No es como el caso anterior, en que el límite es claramente un bit, sino que solo podemos decir que no es infinito, es "menos".
Ahora bien, si establecemos como regla que nuestra máquina no puede conocer de antemano el resultado de un problema, sino que efectivamente debe resolverlo, entonces aplican las reglas que especifiqué antes. Es decir que para poder hacer que una máquina resuelva un problema en un único ciclo se deben dar dos condiciones... o tres:
A- Que la cantidad de elementos del problema sean conocidos con antelación o, teniendo una máquina de cierta capacidad, se puedan completar los elementos faltantes o sobrantes con elementos nulos.
B- Que no existan relaciones cruzadas, es decir que el resultado de un elemento por procesar no afecte el resultado de uno ya procesado.
C- Que el orden de procesamiento de los elementos sea conocido.
Si cualquiera de ésas tres condiciones no se cumple, el problema ya no es resoluble en un único ciclo de mecanismo, sino que se requiere un bucle de cambios de estado y obtener el resultado final progresivamente.
El gran conflicto entre álgebra, aritmética y algoritmos es que el álgebra y aritmética asumen que, si ya se ha demostrado que 5 + 4 es 9, entonces es algo que "se sabe". Pero una máquina normalmente, para cada vez que se le presentan los inputs 5 y 4 para la operación suma, realiza el trabajo de validar que el resultado es, efectivamente, 9. No da nada por asumido EXCEPTO que el algoritmo sea asumir. Por ejemplo: Si para criptografía necesitamos todos los números primos entre 100 y 1000 dígitos, no es conveniente calcularlos todos de nuevo cada vez. Lo mejor es tener un archivo con todos ellos y tomarlos de ahí. Si el archivo está corrupto y/o alguno de los valores que contiene no es número primo, no es asunto de dicho algoritmo.
Pero, de nuevo, no es posible explicarle todo éso al álgebra y, por lo tanto, no se puede obtener una respuesta clara sobre P Vs NP. Porque el álgebra no considera la lógica de los mecanismos y toda respuesta obtenida de ella es potencialmente errónea. No es una cuestión de si todas las variables se tuvieron en cuenta o no, sino que es imposible expresar todas las relaciones existentes entre las variables de forma algebraica. El ejemplo más claro de ello se da en economía, en la "ecuación" PQ = MV, en la cual Q no depende realmente ni de M ni de V, sino de oferta y demanda, que es otro sistema ni siquiera mencionado en la ecuación. Y no es posible expresar eso algebraicamente.

Bueno, he llegado a un veredicto: P NO ES NP, pero el álgebra nunca podría saberlo. Anoche me acordé de algo, y es que en una clase de trigonometría el profe dijo que no se conoce fórmula para calcular el coseno, así que se hace por aproximación. Así que habría simplemente que demostrar que dicha fórmula no podría existir y la aproximación es la única forma.
Pues resulta ser que el coseno no cumple la primera ley de la resolución de problemas en un único ciclo de mecanismo: "Se requiere una cantidad conocida de elementos del problema o que, dada una máquina de cierta capacidad, los elementos sobrantes o faltantes se puedan completar con elementos nulos". El porqué de la ley es obvio: Si no conocés la cantidad de elementos que vas a tener que procesar, tenés que adaptar el algoritmo a cualquier número n, y éso implica un bucle y procesar uno a uno.
Y no se cumple para el coseno, por un lado, porque la curva del coseno posee infinitos valles y crestas, por lo cual no es procesable sino por un bucle. Por el otro lado, si decidiéramos decir que es cíclica, por lo cual solo necesitamos la parte entre 0 y 180 grados... ¿Qué es lo que tenemos en el eje de las x?: Ángulos. Y un ángulo, por definición, es la suma de infinitos segmentos de un círculo. De hecho, ¿Es un ángulo un valor o un mero límite? Como decir "Los segmentos del círculo de acá a acá TIENDEN a sumar 6 grados" porque, le recuerdo, son infinitos segmentos así que nunca se los pudo terminar de sumar. Así que la propia curva de la función coseno proviene de una suma que, por definición, no se puede hacer. Por último, diría que la verdadera fórmula de la función coseno es la que siempre se ha utilizado para aproximarla: Un polinomio infinito. Y en ella, cada punto de la curva depende de la totalidad de los términos del polinomio. No existen elementos nulos o asimilables a nulos en el problema.
Ahora bien... si no es posible crear una máquina que resuelva el coseno en un único ciclo de mecanismo, entonces tampoco es posible crear una fórmula que lo haga. Porque la relación entre ambas cosas es que una fórmula ES un ciclo de mecanismo. Aún cuando las partes internas de la fórmula solo se pudiesen resolver mediante bucles, el conjunto en sí representa un ciclo.
Y a ésto el álgebra no lo podría saber, repito nuevamente, porque el álgebra no tiene en cuenta la lógica de mecanismos.

Ya hce unos años leí en el foro del Rincón Matemático una entrada, acerca del tema de la Compresión de datos maximizada, y me he quedé pensando durante bastante tiempo acerca de la posibilidad de codificar números muy grandes mediante operaciones matemáticas, y convirtiendo la información original en dos claves de reconstrucción de menor tamaño. Y luego actuar, a su vez, sobre estas, recursivamente, disminuyendo una y otra vez el tamaño en bytes de dichas claves.

No hablo exactamente de "compresión de datos", sino de otro concepto algo más abstracto no relacionado directamente con la información, sino con manipulación de números extremadamente grandes.


La idea, nos surgió después de experimentar, como programador, con un software para la encriptación basado en la sustracción, en la resta.


Hace poco tiempo, he vuelto a ver la película Travelling Salesman, sobre la hipótesis de Riemann... y me he quedado pensando en las implicancias políticas económicas, filosóficas, etc. que podría tener la compresión de datos... mucho más allá del límite de Shannon... 🤔

Repito, que no hablo exactamente de "compresión de información" sino de otro concepto, pero que a efectos prácticos podría compararse una cosa con la otra.

Por otra parte, he leído en algunos artículos periodisticos, que hoy el almacenamiento masivo de datos es un negocio muy importante y que mueve en el mundo alrededor (no he confirmado los datos) cerca de 200 mil millones de dólares anuales.

Me gustaría conocer sus opiniones sobre este tema. Un saludo.

Muy interesante el vídeo.

En relación con la compresión de datos, creo que Claude Shannon se equivocó al confundir los átomos y la materia con los datos, que informáticamente solo son número.

Entiendo que el concepto de "compresión" de la información es erroneo, porque los números no pueden "comprimirse" pero sí codificarse.

Creo que mediante el algoritmo adecuado, se pueden codificar números muy grandes conviertiéndolos en cifras mucho más pequeñas, por medio de un proceso recursivo (por ejemplo, codificar 1 Gigabyte en solo 1 Megabyte).

Me gustaría saber que implicancias tendría que se demostrase esta posibilidad de codificación de la información mucho más allá del límite de compresión de Shannon en relación con el tema que trata este interesante video... 🤔
Un saludo.

p es igual y no ala ves que np

video pa mañana que esta muy tarde

Para el 99.99% de los humabos 1 millon de dolares es muchisimo dinero? Dinero del.cual es.muy dificil o directamente imposible de obtener ahorrando.
Pero comparando lo que ganan algunos artistas o deportistas es muy poco.

Like si te chaquetiaste

El otro día me presentaron este problema

¿pueden existir algoritmos de cualquier complejidad superior para un mismo problema?

Me gusta como explicas los videos, además de los elementos gráficos que utilizas. ¿Que tal un video acerca del modelo de Maquina de Turing? Base teórica en la cual se sustentan las computadoras, se que es un tema que se aleja un poco de tu temática, pero igual no deja de ser matemáticas.

Solo entendí el 50% del vídeo xd

😮

I dont speak spanish, but looks looks like a good video

Los algoritmos para resolver ese tipo de problemas se estructuran con bases de datos. ✌🏽

Me encantan este tipo de videos aun sin tener ni idea de matemáticas, pero, mi pregunta es, ¿Se sabe que pueden tener una hipotética solución?

👍

Yo puedo resolver el problema de las reinas polinomicamente

Conclusion: mas MC, menos ajedrez :D

Soy quizas un ignorante mas, pero lo que no ignoro es que todos ven el problema de forma lineal, y no en todas sus dimensiones, al igual que un problema se resuelve por partes, tambien depende de nuestra perspectiva, hay algo simple pero importante que nadie esta notando

Aver si entendi, entonces si consigo crear un programa (digamos las N reinas) en el cual no importa que numero determine como N (asi sea lo mas grande que te puedas imaginar) si la maquina lo resuelve "siempre con el mismo tiempo" en cuestion de segundos, habria comprobado que P=NP? O necesito ver denuevo el video xdd

A sido resuelto?

La parte del gato diciendo hasta luego xd con el tablero grande y ls 8 dams no s epq me dio tanta gracia

No es posible ni será posible porque la lógica dicta que la máquina usara el mecanismo lógico para resolverlo y se apoyara de un ciclo a otro para llegar a la solución sin importar el mecanismo algebraico no interesa si es lineal o no es la lógica suficiente es como querer pedir que NP nunca sea con revision lineal

hay una forma de resolver el problema de las damas generalizado sin exponencial eso lo aprendi jugando en paginas de algoritmos es bastante ingenioso, pero cuando te obligan a empezar con una dama ahi se complica y se usa otro algoritmo que puede no funcionar porque usa la aleatoridad, algo muy curioso es que yo cuando me empezó a gustar los algoritmos yo me hice la misma pregunta, de si hay alguna razon por la que es imposible completar cualquier problema en un tiempo relativo a el tamaño de las entradas, lo intente resolver pero es como intentar atrapar un gas con una canasta, me entere hace poco que el problema ya se conocía y parece ser aun mas dificil de que me imagine, muy buen video

P = NP y te lo demuestro.

Tenía una duda y era si con "problema" te refieres a cualquier "problema". Osea "P vs NP" es un problema del tipo P o del tipo NP?

Laikazo por decir computación y no informática.

Aquí la respuesta P≈NP

killer creeper, me ayudas a hacer netherigedon pls

Hola MatesMike:
Un saludo muy grande. Tu puedes encontrar el número del millón porque conoces la matemática . Yo (79 años) te pado el secreto, pero vamos a medias; bueno me conformo con un 25%. Contacteme.
Un abrazo cósmico. Abarca-El-Raja

MIKE Buenos videos broo 🔥
Aureo + 2 es primo?